Mensajes

NADA de tomas aéreas he dicho! XD

gracias do-while! vamos con esa! voy a extender el programa... ya llegué a mi casa, tengo 1,5l de te negro listos y 250g de maní japonés! ese código sale en un rato!

ikillnukes tambien a eso voy, segundo argumento sin salida, solo para ver el tiempo del calculo, los decimales calculados correctos no es tan simple fijate que yo genero decimales de mas, para asegurar el valor correcto, si ves.el metodo de euler ves que casi siempre da decimales periódicos

próximo a probar:salida concatenada a archivo, tiempo de ejecución, alguna sugerencia?

en realidad no me preocupé del cout porque la diferencia ue causa es baja, si calculan 10000 decimales, haces unos 33000 calculos con 3 variables de 35kb xD e imprimir 35kb no toma sino unas décimas de segundo por lento que sea :p pero lo voy a hacer con printf me dió pereza hacerlo anoche

por otro lado no se puede hacet cifra a cifra ya que el resultado es la combinación de factoriales sumatorias y potencias, el numero siempre debe debe ser reusado

[---------------------------------------------------------------codigo final con formulas a partir de aqui---------------------------------------------------------------]

Buenas, en estos días estaba por aquí un alguien preguntando sobre un programa básico con pi, por cosas de la vida, decidí ahondar en el tema... calcular pi con alta precisión...

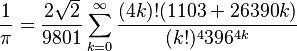
deja claro que el siguiente tema no lo hago en pro de discutir la naturaleza de pi, ni nada al respecto, es solo en pro del calculo de alta precisión

aquí básicamente solo hay 2 temas importantes que abordar

-¿qué formula usar?
-¿como calculo números en alta precisión?

con lo primero... la formula, decidí usar la de euler

escogí esta por su precisión y su relativamente fácil aplicación

para aplicarla la tenemos que separar en 2 partes por su sumatoria y su factorial...

Código (cpp) [Seleccionar] Expandir


sumatoria = factorial = 1;
for(i=1;i<ciclos;i++){
   factorial *= i/(i*2+1);
   sumatoria += factorial;
}
sumatoria *=2;
pi = sumatoria


ahí resolvemos esa formula básicamente... pero nos damos cuenta de un problema... los numeros double están limitados a 64 bits... unos 20 decimales para nuestro caso...

en este caso viene la aritmetica de alta precisión, GMP... aquí en el foro buscaba como usarlo... al final conseguí y publiqué el como...

este usa unidades especificas y operaciones especificas para alta precisión...

doy una ligera explicación de lo usado... no voy a caer en mucho detalle de las funciones...
mpf_t es una variable de tipo "float" propia
mpf_set_default_prec da el valor en bytes que la variable usará
mpf_init_set_str inicializa las variables desde un string... por que un string? porque quise -.-... se hay que inicializar las variables obligatoriamente

mpf_set_ui da un valor desde un entero sin signo a un float
div= division, mul = multiplicaccion, add= adición

mpf_get_str convierte de float de GMP a char* (string)

como no habia una multiplicacion / asignacion directa, me tocó usar una variable de intercambio


ahora la parte interesante... el codigo  

hice un pequeño/bonito formato de impresión de 10 en 10 dígitos... en  lineas de 50 y bloques de 500 con el numero de dígito como indicador... probé solo hasta 40.000 dígitos, comprobando en internet precisos... pero en 5min 9 seg! es mi único intento en este campo... no esperen romper el record mundial de decimales ;P por cierto... de ahí en adelante, los dígitos son cuesta arriba... así que cuidado con el tiempo... pueden usar el programa pasando el numero de dígitos como argumento... los dígitos los toma en cuanta de 100 en 100

pd: la precisión la hago como  "precision = digitos * 100 * 3 * 1.12" porque descubrí que se requieren 3 ciclos por dígito correcto sobre los 100 con un 12% de error (calculado a ojo)

---------------------------------------------------------------codigo final con formulas a partir de aqui---------------------------------------------------------------

librerias

Código (cpp) [Seleccionar] Expandir

#include <iostream>
#include <stdlib.h>
#include <string>
#include <gmp.h>
#include <gmpxx.h>
#include <time.h>
#include <sstream>
using namespace std; // :P


prototipos

Código (cpp) [Seleccionar] Expandir

string metodo_euler(unsigned long int digitos, mp_exp_t &exponente);
string metodo_ramanujan(unsigned long int digitos, mp_exp_t &exponente);
void imprimir_pi_aux(string pi, mp_exp_t exponente, int digitos);

main

Código (cpp) [Seleccionar] Expandir

int main(int argc, char **argv) {
   unsigned long int digitos = strtol(argv[1], NULL, 10); //argv a int
   mpf_set_default_prec(32 * 10 * (digitos / 100) * 1.11); //precision + 10%
   long exponente;
   clock_t start = clock();
   string pi;
   int metodo = 0;
   int i = 1;
   for (i = 0; i < argc; i++) {
       if (argv[i][0] == '-') {
           switch (argv[i][1]) {
               case 'e':
                   metodo = 0;
                   break;
               case 'r':
                   metodo = 1;
                   break;
           }
       }
   }
   switch (metodo) {
       case 0:
           cout << "imprimiendo por metodo Euler, " << digitos * 3 * 1.12 << " ciclos"<<endl;
           pi = metodo_euler(digitos, exponente);
           break;
       case 1:
           cout << "imprimiendo por metodo Ramanujan, " << (int) (digitos / 8 * 1.01) << " ciclos"<<endl;
           pi = metodo_ramanujan(digitos, exponente);
           break;
   }

   clock_t end = clock();

   imprimir_pi_aux(pi, exponente, digitos);
   cout << "\ntiempo total de ejecucion: " << (float) (end - start) / CLOCKS_PER_SEC << "\n";
   cout << "tiempo total de impresion: " << (float) (clock() - end) / CLOCKS_PER_SEC << "\n\n";
   return 0;
}

tiene 2 argumentos... primero los digitos (obligatorio)... luego -r para ramanujan o -e para euler (opcional, euler predeterminado)

imprimir_pi_aux

para tener un formato único de impresión para todo

Código (cpp) [Seleccionar] Expandir

void imprimir_pi_aux(string pi, long exponente, int digitos) {
   cout << "Pi: ";
   stringstream aux;
   unsigned long int i;
   if (exponente <= 0) {
       cout << "0.";
       while (exponente < 0) {
           cout << 0;
           exponente++;
       }
   } else {
       for (i = 0; i < exponente; i++) {
           cout << pi[i];
       }
       cout << ".\n\n1:\t";
   }
   for (i = exponente; i < digitos + 1; i++) {
       aux << pi[i];
       if ((i - exponente + 1) % 10 == 0) aux << ' ';
       if ((i - exponente + 1) % 500 == 0) aux << endl;
       if ((i - exponente + 1) % 50 == 0 && i < digitos) aux << endl << i + 1 << ":\t";
   }
   aux << endl;
   cout << aux.str();
}
aux por consejo de amchacon

metodo_euler

corto, simple, pero largo... para 10.000 dígitos 33.600 ciclos o para mi unos 11 seg

basado en la formula

Código (cpp) [Seleccionar] Expandir

string metodo_euler(unsigned long int digitos, long &exponente) {
   digitos /= 100; //trabaja con lotes de 100
   unsigned long int precision = digitos * 100 * 3 * 1.12;
   unsigned long int x, i;
   mpf_t factorial, sumatoria, buff_factorial; //variables GMP
   mpf_init_set_ui(factorial, 1); //factorial=1
   mpf_init_set_ui(sumatoria, 1); //sumatoria=1
   mpf_init_set_ui(buff_factorial, 1); //buff_factorial=1

   for (x = 1; x < precision; x++) {
       i = 2 * x + 1;
       mpf_set_ui(buff_factorial, x); //buff_factorial=x
       mpf_div_ui(buff_factorial, buff_factorial, i); //buff_factorial*=i
       mpf_mul(factorial, factorial, buff_factorial); //factorial*=buff_factorial
       mpf_add(sumatoria, sumatoria, factorial); //sumatoria+=factorial
   }
   mpf_mul_ui(sumatoria, sumatoria, 2); //sumatoria*=2
   return mpf_get_str(NULL, &exponente, 10, 0, sumatoria);
}

metodo_ramanujan

por consejo de do-while, basado en la formula

eficiente, pero dificil de aplicar (si no, miren el codigo de abajo)
para 10.000 digitos 1.262 ciclos en 1.1 segundos

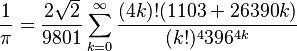
Código (cpp) [Seleccionar] Expandir

string metodo_ramanujan(unsigned long int digitos, long &exponente) {
   digitos /= 8;
   digitos *= 1.01;
   unsigned long int i, j;
   mpf_t sumatoria, buff_sumatoria, buff_ciclo_superior, buff_ciclo_inferior, primera_parte,
           buff_ciclo_inferior2, factorial_superior, factorial_inferior;
   mpf_init_set_ui(sumatoria, 1103); //sumatoria=0
   mpf_init_set_ui(buff_sumatoria, 0); //buff_sumatoria=0
   mpf_init_set_ui(buff_ciclo_superior, 0); //buff_ciclo_superior=0
   mpf_init_set_ui(buff_ciclo_inferior, 0); //buff_ciclo_inferior=0
   mpf_init_set_ui(primera_parte, 0); //primera_parte=0
   mpf_init_set_ui(buff_ciclo_inferior2, 0); //buff_ciclo_inferior2=0
   mpf_init_set_ui(factorial_superior, 1); //factorial_superior=1
   mpf_init_set_ui(factorial_inferior, 1); //factorial_inferior=1
   mpf_sqrt_ui(primera_parte, 2); //primera_parte=sqrt(2)
   mpf_mul_ui(primera_parte, primera_parte, 2); //primera_parte*=2
   mpf_div_ui(primera_parte, primera_parte, 9801); //primera_parte/=9801

   for (i = 1; i <= digitos; i++) {
       for (j = (i - 1)*4 + 1; j <= i * 4; j++) {
           mpf_mul_ui(factorial_superior, factorial_superior, j);
       }
       mpf_set_ui(buff_ciclo_superior, 26390);
       mpf_mul_ui(buff_ciclo_superior, buff_ciclo_superior, i);
       mpf_add_ui(buff_ciclo_superior, buff_ciclo_superior, 1103);
       mpf_mul(buff_ciclo_superior, buff_ciclo_superior, factorial_superior);
       mpf_mul_ui(factorial_inferior, factorial_inferior, i);
       mpf_pow_ui(buff_ciclo_inferior, factorial_inferior, 4);
       mpf_set_ui(buff_ciclo_inferior2, 396);
       mpf_pow_ui(buff_ciclo_inferior2, buff_ciclo_inferior2, 4 * i);
       mpf_mul(buff_ciclo_inferior, buff_ciclo_inferior, buff_ciclo_inferior2);
       mpf_div(buff_sumatoria, buff_ciclo_superior, buff_ciclo_inferior);
       mpf_add(sumatoria, sumatoria, buff_sumatoria);

   }
   mpf_mul(sumatoria, sumatoria, primera_parte);
   mpf_ui_div(sumatoria, 1, sumatoria);
   return mpf_get_str(NULL, &exponente, 10, 0, sumatoria);
}

localizar la ubicación... no... ni si quiera el mismo fb lo podría saber... la operadora es quien podría dar más seguridad pero dudo que nada más preciso que un circulo en un par de km de radio :stal vez si el teléfono es samsung o alguna marca importante, la empresa podría intentarlo...

efectivamente apoyo a Eternal Idol...

no coloques los títulos en mayúsculas! -.-

no escribas en mayúsculas... :s es de "mal gusto", busca en el foro en la sección de ingeniería inversa los tutoriales

cierto! XD pensé que era el foro de programación general! XD leí mal!


puedes aplicar la de  Gh057... y para hex y oct es facil desde binario para octal agarras de 3 en 3 bits de binario, para hex agarras de 4 en 4